Earlier this year, I interviewed with a well-known tech startup, one of the hundreds of companies that claims to have harder interviews, more challenging work, and smarter employees than Google. My first interviewer, John, gave me the standard tour: micro-kitchen stocked with a combination of healthy snacks and candy; white male 20-somethings gathered around a foosball table; bright spaces with cutesy themes; a giant TV set up for video games; and the restroom. Finally, he showed me a closet-sized conference room and we got down to business.
After the usual data structures and algorithms song and dance, we moved on to the main question: how would you design a classification system for foo? We had a discussion about design tradeoffs, but the key disagreement was about the algorithm. I said, if I had to code something up in an interview, I'd use a naive matrix factorization algorithm, but that I didn't expect that I would get great results because not everything can be decomposed easily. John disagreed – he was adamant that PCA was the solution for any classification problem.
We discussed the mathematical underpinnings for twenty-five minutes – half the time allocated for the interview – and it became clear that neither of us was going to convince the other with theory. I switched gears and tried the empirical approach, referring to an old result on classifying text with LSA (which can only capture pairwise correlations between words) vs. deep learning. Here's what you get with LSA:
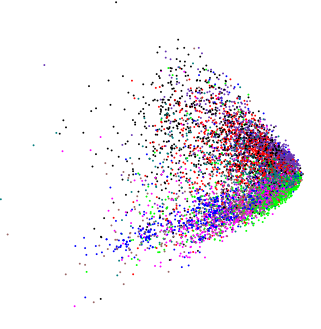
Each color represents a different type of text, projected down to two dimensions; you might not want to reduce to the dimensionality that much, but it's a good way to visualize what's going on. There's some separation between the different categories; the green dots tend to be towards the bottom right, the black dots are a lot denser in the top half of the diagram, etc. But any classification based on that is simply not going to be very good when documents are similar and the differences between them are nuanced.
Here's what we get with a deep autoencoder:
It's not perfect, but the results are a lot better.
Even after the example, it was clear that I wasn't going to come to an agreement with my interviewer, so I asked if we could agree to disagree and move on to the next topic. No big deal, since it was just an interview. But I see this sort of misapplication of bog standard methods outside of interviews at least once a month, usually with the conviction that all you need to do is apply this linear technique for any problem you might see.
Engineers are the first to complain when consultants with generic business knowledge come in, charge $500/hr and dispense common sense advice while making a mess of the details. But data science is new and hot enough that people get a pass when they call themselves data scientists instead of technology consultants. I don't mean to knock data science (whatever that means), or even linear methods. They're useful. But I keep seeing people try to apply the same four linear methods to every problem in sight.
In fact, as I was writing this, my girlfriend was in the other room taking a phone interview with the data science group of a big company, where they're attempting to use multivariate regression to predict the performance of their systems and decomposing resource utilization down to the application and query level from the regression coefficient, giving you results like 4000 QPS of foobar uses 18% of the CPU. The question they posed to her, which they're currently working on, was how do you speed up the regression so that you can push their test system to web scale?
The real question is, why would you want to? There's a reason pretty much every intro grad level computer architecture course involves either writing or modifying a simulator; real system performance is full of non-linear cliffs, the sort of thing where you can't just apply a queuing theory model, let alone a linear regression model. But when all you have are linear hammers, non-linear screws look a lot like nails.
In response to this, John Myles White made the good point that linear vs. non-linear isn't really the right framing, and that there really isn't a good vocabulary for talking about this sort of thing. Sorry for being sloppy with terminology. If you want to be more precise, you can replace each mention of "linear" with "mumble mumble objective function" or maybe "simple".